Median Filtering in Spatial Domain in Image Processing

Median Filtering in Spatial Domain: A non-linear digital filtering method called the median filter is frequently used to enhance quality of image by eliminate the noise from an image. This kind of noise reduction is a common pre-processing procedure to enhance the outcomes of subsequent processing. It has uses in both signal processing and digital image processing, median filtering is frequently employed to preserve edges while reducing noise in specific circumstances.

Advantage of Median Filter over Linear Filter: In addition to signal processing, time series processing, and image processing, median filters are frequently employed as smoothers. The ability of the median filter to completely eliminate the impact of input noise values with exceptionally large magnitudes is a significant advantage it has over linear filters.

How median filter works in image processing? The median filter operates by going pixel-by-pixel across the image and replacing each value with the median value of nearby pixels. The "window" is a pattern of neighbours that moves pixel by pixel over the entire image.

Algorithm of Median Filter:
1. Read input image.
2. Store the pixel values of input image in an array.
3. For each pixel value store all the neighbor pixel value including that cell in a new array (called window).
4. Sort the window array.
5. Median of window array is used to store output image pixel intensity.


Example 1] Apply Median (3X3) filter on a given image f(x,y).
Use (a) Pixel Replication for Padding
(b) Zero padding
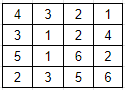
Consider the following image:

Answer:
f(x,y)=

Median Mask=h(x,y)=

Median filtering means convolue the image with the empty mask.
Before convoluition to cover the boundary pixels, we can do pixel replication or zero padding as follows:
(a) Pixel replication:
Here we replicate last column to the right, first column to the left, first row on upward side and last row on downward side.

(b) Zero Padding: Here we pad zeros to the right of last column, to the left of first column, on top of first row and below.

Use Pixel replicated image to perform the median filtering with the help of the mask.

Step 1) Now, place the mask over first row and first column and consider all the pixel under the mask for median calculation for the candidate pixel. To achieve this we need to arrange pixels under consideration in ascending or descending order and then find the median. At last replace this median value with the candidate pixel.

Step 2) Shift the mask from first column to second column and continue the process of step 1)

Step 3) Continue above steps till last pixel is considered.

Step 4)

Step 5) After completing first row move the mask to second row and repeat above steps to obtain candidate pixel using median filter.

Zero Padding Method:

We follow same procedure as above to obtain the output image.

MATLAB Program for Median Filter.

% Median Filters
I=imread('LeenaRGB.jpg');
K = rgb2gray(I);
J= imnoise(K ,'salt & pepper',0.05);
f= medfilt2(J,[3,3]);
f1=medfilt2(J,[10,10]);
subplot(3,2,1); imshow(I); title('Original Image');
subplot(3,2,2); imshow(K); title('Gray Image');
subplot(3,2,3); imshow(J); title('Noise added Image');
subplot(3,2,4); imshow(f); title('3x3 Image');
subplot(3,2,5); imshow(f1); title('10x10 Image');
OUTPUT: